

The lim u→0 has no reason or right to be there.

So the final substitution of e for lim u→0(1 + u) 1/u is illegal. The mathematicians write down the brackets and then ignore them, transferring the limit inside them to suit themselves. In fact, this is what the brackets mean in the term With the term lim u→0(1 + u) 1/u we are monitoring only the sum and exponent as we approach the limit. With the term lim u→0, we are monitoring the natural log as we approach the limit. Because they are not equivalent, we can see that shifting the lim n→0 is not just a matter of preference.
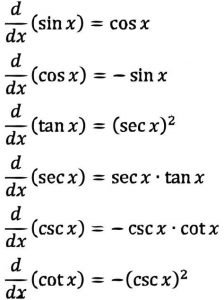
This is important, because as confirmation of the last step, we are sent to the “definition” of e: You cannot separate the ln from its number. Lim u→0 = 1/x ln Īs they pull the 1/x down from the exponent and put it in front of the ln (which is legal) they also shift the lim u→0 forward, so that it is now in front of the ln (which is not legal). It is false because it contains huge errors, errors I can point out very easily. The derivative for the natural log is currently found by this method: I will continue to put up what I have as I discover it, and if some of turns out to be wrong, well, so what. But since the calculus has been incomplete for centuries, perhaps millennia, I do not feel especially pressed to apologize. My corrections to the calculus are incomplete and will remain incomplete for many months or years, no doubt. For this reason, these latest papers are not proof that I am contrary and crazed, they are just one more indication that I have the courage to go where my nose leads me, the consequences be damned. All the modern maths are based on the calculus, and a problem with the calculus would infect every manipulation that depends upon it.

These problems include the cause of the need for renormalization, the cause of the failure of unification, and the cause of all the point problems in both QED and GR. In my theoretical research over the last decade, I have come to the conclusion that many of the problems in QED and GR are caused by fundamental and long-standing disclarities in the calculus. These papers have only been up about a week, but I can already see the firestorm ahead. I have been prodded by recent events to add an introductory paragraph here, explaining why I would want to attack the calculus. In doing so, I will show the magnificent cheat in the current derivation of dln(x)/dx, embarrassing every living mathematician. The Natural Log and of 1/x by Miles MathisĪbstract: I will show that the current derivative of the natural log and the current derivative of 1/x are both wrong.


 0 kommentar(er)
0 kommentar(er)
